R語言的決策樹應用

決策樹，是一種統計學與機器學習會用到的分群方法，若想要預測的變數為類別變數則可稱分類樹(classification tree)，若想要預測的變數為連續型變數則稱回歸樹(regression tree)。決策樹也就是常常聽到的 CART (Classification And Regression Trees)，其中的原理就是利用衡量亂度的指標 impurity function 來衡量資料的亂度並且將其最小化，結果就會產生一連串的分群，也就是這個資料集所能產生最大的決策樹，接下來考慮誤差與節點太多所產生的成本問題，進行截樹，最後產生一個精簡且解釋力強的決策樹模型。

在R語言上的應用可以使用tree的套件來進行，以大家常用的R語言開放資料 “iris" 為例。iris 紀錄了鳶尾花的品種與花萼花瓣的長度與寬度的資料，小編就利用花萼花瓣的長度寬度來建立品種的分類模型。

> library(tree)
> library(datasets)
> data("iris")
> dim(iris)
[1] 150   5

> colnames(iris)
[1] "Sepal.Length" "Sepal.Width"  "Petal.Length" "Petal.Width"  "Species"   
  
> tmax <- tree(Species ~ Sepal.Length + Sepal.Width + 
+                 Petal.Length + Petal.Width, data = iris)
> plot(tmax)
> text(tmax)

這即是最大的決策樹，再利用交叉驗證 (cross-validation) 來計算類似誤差的統計量deviance，並計算相對應節點數的 k值 (cost of complexity)，簡單來說就是每增加一個節點而增加的成 本，是用來控制決策樹有幾個節點。因為交叉驗證是利用抽樣分成訓練資料集與測試資料集的概念，所以如果要防止每次做的情況會有微小的差異，請愛用set.seed()函數。

> set.seed(5566)
> tcv <- cv.tree(tmax)
> plot(tcv)

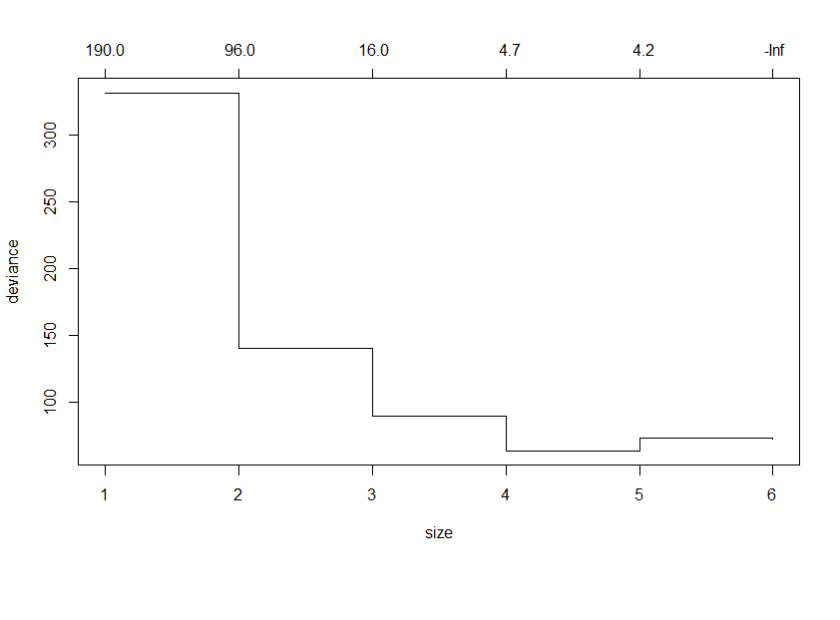
由圖可以知道在節點數到了3之後就下降緩慢，所以如果想要讓決策數停在節點數為3的話，就要設定k值介於16至95之間，就能建立一個精簡且解釋力不會下降太多的決策樹。

> tree.prune <- prune.tree(tmax , k = 80)
> plot(tree.prune)
> text(tree.prune)

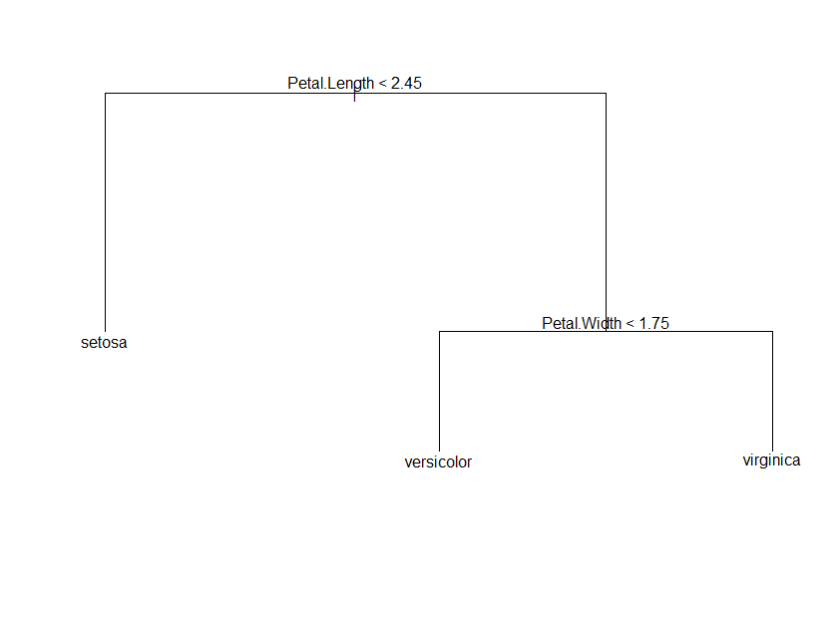
從最後三個節點的決策樹圖就可以做簡單的預測，如果花瓣長度小於2.45就可分類為setosa，若花瓣長度大於2.45則再依據花瓣寬度來判斷品種。由數據顯示，花萼的長度寬度與鳶尾花的這三種品種沒有顯著的連動關係。