大台指期貨報酬分配

2016 年 09 月 26 日 long.jian 程式交易發表留言

財務理論常常提醒讀者們，報酬率的分佈具有高狹峰及厚尾的特性，這篇試著驗證大台指期貨之報酬率分佈是否具這樣特性，及展示使用常態分配與廣義誤差分配 (generalized error distribution) 配適報酬率之情況，其中廣義誤差分配可以模擬高狹峰的特徵。

對數報酬:

本篇文章使用的是對數報酬，在假設連續時間的情況下，報酬率為連續利率，故使用對數報酬。

$r_t = log( S_t / S_{t-1} )$

$S_t$ : 第 t 期商品價格

$r_t$ : 第 t 期報酬率

廣義誤差分配 ( generalized error distribution ):

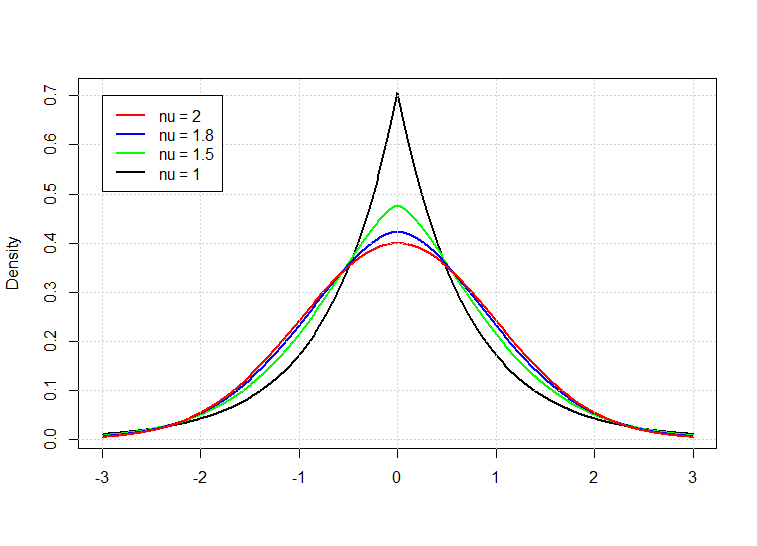
廣義誤差分配增加了 $\nu$ 形狀參數，使得模型可以模擬高狹峰及厚尾情況，廣義誤差分配 (generalized error distribution) 機率密度函數如下:

$\displaystyle f(x) = \frac{ \nu}{2 \sigma \Gamma( \frac{1}{ \nu})} e^{-( \frac{|x- \mu|} { \sigma} )^{ \nu}}$

其中 $\nu$ 為形狀參數，當 $\nu = 2$ 時為常態分配。接著觀察不同 $\nu$ 情況下機率分佈的情況。可以觀察到當 $\nu$ 越小峰度越高的情況，並且具有厚尾情況。

ged_nu

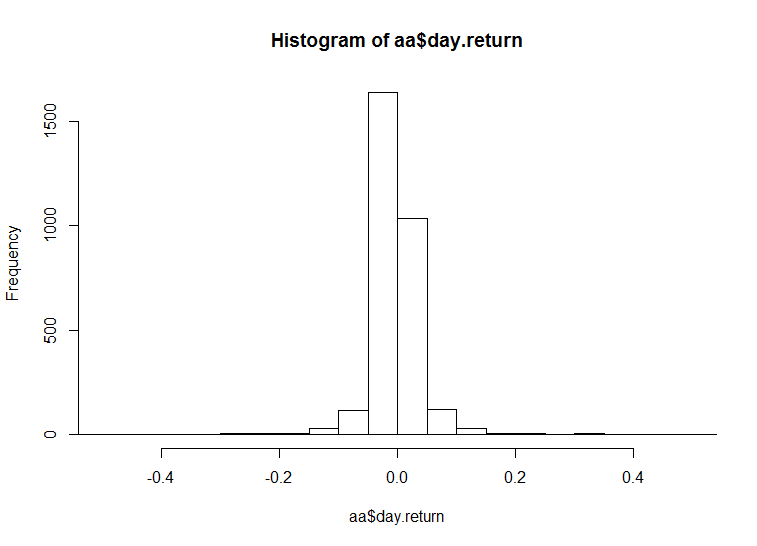
實際資料配適

這裡使用 2001/01/02 至 2016/07/21 大台指期貨分鐘資料，使用每分鐘收盤價計算對數報酬，累積分佈如下，明顯可以觀察高狹峰情況。

return_hist

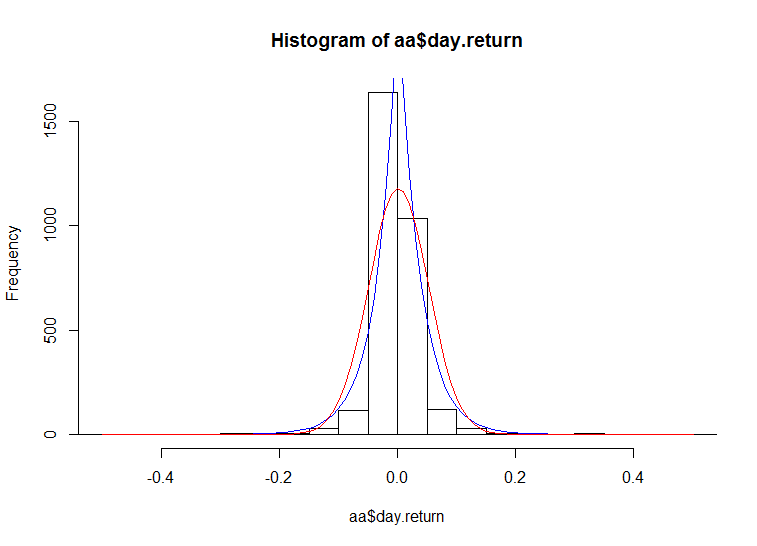
接著配適常態分配與廣義誤差分配，常態分配參數估計使用最大概似估計量 $\hat{ \mu} = \sum_{i = 1}^n x_i$ , $\hat{ \sigma} = \frac{1}{n} \sum_{j = 1}^n (x_j- \hat{ \mu} )^2$ 。配適結果為紅色的線。廣義誤差分配的最大概似估計量並沒有封閉解，故使用近似最大概似估計法，計算最大概似估計量的數值解。配適結果為藍色的線。可以發現廣義誤差分配配適的情況更好，較接近真實資料。

return_hist_fit

結論

根據大台指期貨所算出的對數報酬，的確如財務理論所說的具高狹峰與厚尾情況，所以如果想使用數學統計模型估計大台指期貨價格的話，建議使用廣義誤差分配模型作為模型假設較為精準。

發表迴響取消回覆